Category: Lego Maths

Posted on

Daily Lego Maths: Day 10

Here is a table and chair made from red and blue bricks. How many red bricks can you see? How many blue bricks?

Explore how many red and blue bricks you would need to make different sets of tables and chairs!

A lego chair and table made from red 4 by 2 and blue 2 by 2 bricks. The table is made from 2 red and 2 blue bricks, and the chair from 3 blue and 1 red brick

Posted on

Daily Lego Maths: Day 9

Is there more yellow, more red, or both the same?
Is this part of a pattern? How might the pattern continue?
How many bricks will there be in the next pattern?

7 columns of red and yellow bricks to make a symmetrical lozenge. The columns alternate red and yellow, and have 1, 2, 3, 4, 3, 2, 1 brick in.

What other mathematical questions could you explore?

Posted on

Daily Lego Maths: Day 8

The pattern below has 7 rows of red and yellow bricks.
Can you work out the sequence?
Can you describe what the eighth row would look like?

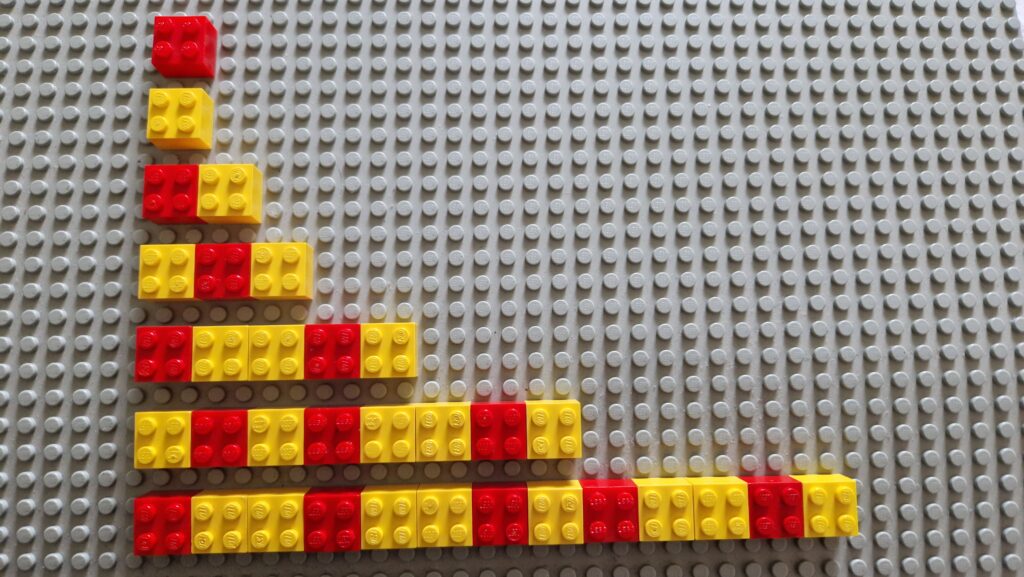
7 rows of bricks, getting longer. Row 1: R Row 2: Y Row 3: R Y Row 4: Y R Y Row 5: R Y Y R Y Row 6: Y R Y R Y Y R Y Row 7: R Y Y R Y Y R Y R Y Y R Y

Is there a quick way to work out how many reds and yellows you would need for future rows?

Posted on

Daily Lego Maths: Day 7

Here is a ‘circle’ made out of Lego. It’s not very circular!
What questions might a mathematician ask?

An approximation to a circle made from red and yellow 2 by 2 lego bricks. The pattern has mirror symmetry horizontally and vertically. There are ten rows of bricks, with 2, 6, 8, 8 and 10 bricks in the first five rows and then descending 10, 8, 8, 6, 2. The boundary of the shape is yellow and the middle is red.


What is the ‘radius’ of this circle? What is the area?
How could you make a better circle out of Lego?

Posted on

Daily Lego Maths: Day 6

Are there more blue bricks or white bricks? Can you work it out without counting?

This is a 3 by 5 pattern. Can you work out how many blue and how many white bricks you would need for other sizes of pattern?

Have you ever seen other patterns like this?

A pattern made of 3 rows of 5 2 by 2 lego bricks. The top and bottom row both alternate blue-white-blue-white-blue, and the middle row alternates white-blue-white-blue-white
Posted on

Daily Lego Maths: Day 4

What do you notice?
What do you wonder?

If this shape was part of a sequence, what position in the sequence might it be? What other shapes would appear in the sequence?

Is there a quick way to work out how many bricks you would need for different shapes in the sequence?

A cross-shaped pattern made out of 2 by 2 lego bricks. The centre of the cross is a single white brick. Around that are four black bricks. Blue bricks then go into the eight spaces around the black bricks, and finally there is a ring of twelve red bricks around the blue bricks.
Posted on

Daily Lego Maths: Day 3

Here are two animals made out of lego. (What animals could they be?)
Can you describe or build the next animal in the sequence?
How many red bricks would you need?
How many blue bricks?
How many yellow bricks?
How many black bricks?

Two animalesque figures made from lego. They are viewed side on. They are made from bricks of width 2, overlapped so that the model stays together. Each shape consists of a 'body' made from two rows of red bricks, 'legs' made from yellow bricks, a tail made from a single black brick and a 'head' made from a diamond shape of blue bricks.

Can you predict how many bricks of each colour you would need if the sequences continued?

Can you make some Lego animal sequences of your own?

Posted on

Daily Lego Maths: Day 2

Here is the fourth pattern in a sequence made of Lego.

What do you notice?
What do you wonder?
What questions might a mathematician ask?

A pattern of Lego bricks on a grey baseboard. The pattern is made of two by two square bricks. In the top left corner is a single black brick. To the right is a white brick, and then two white bricks are immediately below the black and white. Below that there is a row of 3 blue bricks which wraps up and to the right, five blue bricks altogether. Finally there are yellow bricks on the bottom row and down the right hand side so the whole picture is four bricks by four bricks.

Can you draw or make the next pattern in the sequence?
How many bricks are there of each colour? How many bricks will you need of the next colour?