Articles

Posted on

Daily Lego Maths: Day 21

What do you notice?
What do you wonder?

How would you describe this shape to someone who couldn’t see it?
Is there more yellow or red? How do you know?

A shape made out of red and yellow 2 by 2 lego bricks. The shape has a vertical line of symmetry. There are five rows of bricks, with rows of length 2 centred at the top and bottom, and rows of length 4 in the middle. The colourings are as follows: Row 1: R Y Row 2: Y Y R R Row 3: Y R Y R Row 4: Y Y R R Row 5: R Y

What other mathematical questions could you explore?

Posted on

Daily Lego Maths: Day 20

Here is a picture made from Lego. Can you tell what it is?
How do you think it was designed?
What mathematical questions does this picture provoke for you?

Pixel-art football made out of black and white lego bricks on a grey baseboard

Why not try making some similar lego art of your own?

Posted on

Daily Lego Maths: Day 19

Here are two shapes each made from 5 square blocks.

Two shapes each made out of five 2 by 2 bricks on a grey baseboard. There is a blue shape with three blue bricks in a horizontal row and a blue brick above and below the rightmost brick. There is a white shape with three bricks in a column with a brick to the left of the bottom brick and a brick to the right of the middle brick.

What other shapes could you make by joining 5 squares in this way?
How many are there altogether?
How can you be sure you found them all?

Posted on

Daily Lego Maths: Day 18

Here is a pattern made from red and yellow bricks.
Can you describe the pattern? What mathematical questions could you ask?

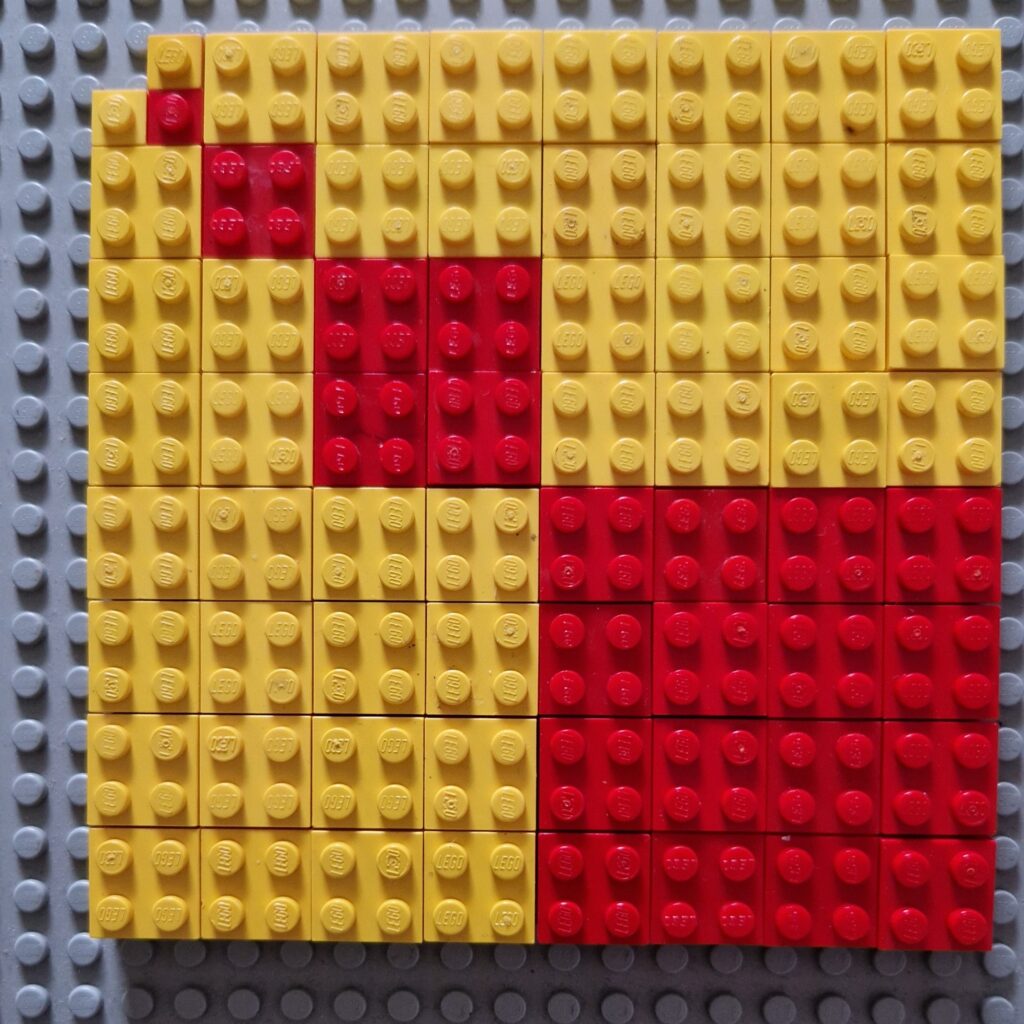
A 16 by 16 lego square made up as follows: Top right and bottom left 8 by 8 grids each made from 16 2 by 2 yellow bricks. Bottom right is another such 8 by 8 grid made in red. The top left corner of the grid is made in the same way but with two yellow and one red 4 by 4 squares, and the top left corner of that square is made by two yellow and one red 2 by 2 bricks. Finally the very top left has 1 by 1 yellows in the top right and bottom left, and a 1 by 1 red in the bottom right.

What fraction of the shape is yellow? How do you know?

Posted on

Daily Lego Maths: Day 17

A Triomino is a shape made from three squares joined together. There are two types of triomino, a straight line and an L shape.
You can make L triominoes out of lego by putting together a 4 by 2 and a 2 by 2 brick, with the same underneath but the other way round to keep it together.

Here is an L triomino and a shape made out of L triominoes. What do you notice?

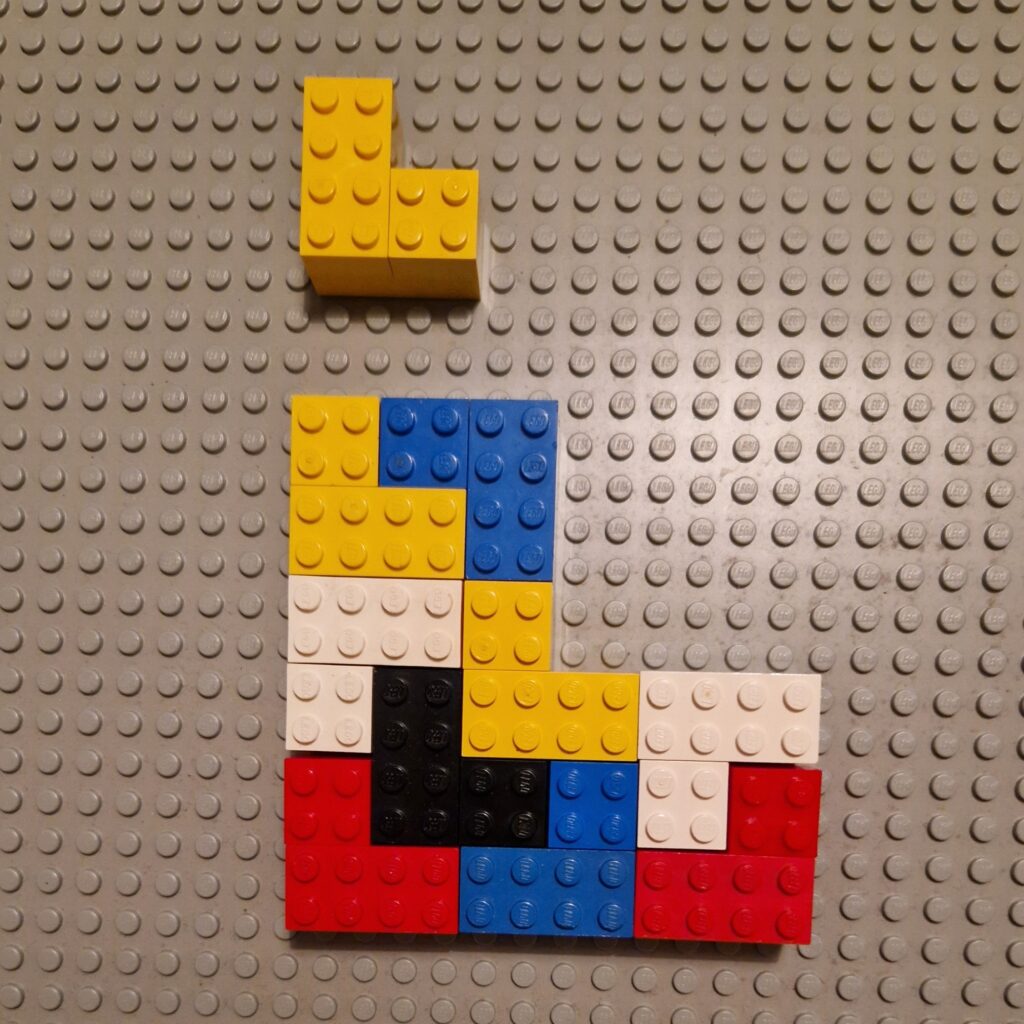
Two L shapes made out of Lego. The top L consists of a 4 by 2 brick with a 2 by 2 brick adjacent, held together with bricks underneath. The bottom L is made up of 9 such Ls, joined to make an enlargement with scale factor 3 of the original.

The L triomino is a rep-tile, which means you can make larger copies of the tile using lots of small tiles. Here are some questions to explore:
By what scale factor has the L triomino above been enlarged?
How many tiles were needed?
Can you find a way to make other enlargements of the original?
Is it possible to make an enlargement of the original using any whole number scale factor?
Can you find any other Lego rep-tiles?

Posted on

Daily Lego Maths: Day 16

Here is a bus made from Lego. What mathematical questions could you explore?

Lego bus made from red and blue bricks, viewed from the side.Two wheels are visible at the bottom; perhaps there are two more wheels on the other side of the bus. The blue bricks make three 'windows' at the front, back, and middle.

How many wheels?
How many windows?
Might there be wheels and windows that you can’t see?

A bigger bus might have more wheels and windows. Can you draw or make some more Lego buses? How many windows would there be? How many wheels?

Posted on

Daily Lego Maths: Day 13

***Spoilers for Day 12 ahead***

Here are the seven possible tetrominoes you can make by joining together four squares edge to edge.

7 possible shapes made from joining four square bricks together edge to edge.

Is it possible to tile a 7 by 4 rectangle with these seven pieces?

Posted on

Daily Lego Maths: Day 12

Here are two shapes. What’s the same? What’s different?

Two shapes made out of four 4 by 4 square bricks. The white shape has two bricks together and then a row of two bricks offset to the left below. The blue shape is the same but offset to the right instead of the left.

How many different shapes can you make with 4 square bricks?
How will you know that you have found every possibility?

What if you use 5 bricks instead?