Last weekend, it was Big MathsJam, and among the mathematical delights I sampled, there was a talk by Christian Lawson-Perfect about stacking cups. You can see a really quick version of his talk on the Aperiodical website. Before reading on, you might like to think about the problem a bit…
Christian suggested in his talk the well-known sequence that emerges as you explore this problem, but in a five-minute talk there wasn’t time to explore why. So in the car on the way home from mathsjam, and again in the car on the way to work, I tried to figure out what was going on structurally, and how that could explain the sequence.
Let’s start by considering a different problem entirely. It’s quite a well-known problem, so you might have met it before. Imagine we have a species of rabbit where a mating pair takes 1 month to reach maturity, produces 1 new mating pair every month, and lives forever. If we started with 1 mating pair, how do we calculate the number of rabbits after n months?
Let’s draw a table.
| Month Number | # of Adults | # of Babies | Total Rabbits |
| 1 | 1 | 0 | 1 |
| 2 | 1 | 1 | 2 |
| 3 | 2 | 1 | 3 |
| 4 | 3 | 2 | 5 |
| 5 | 5 | 3 | 8 |
| 6 | 8 | 5 | 13 |
| 7 | 13 | 8 | 21 |
| 8 | 21 | 13 | 34 |
In general, suppose last month there were a adults, b babies, and r=a+b rabbits in total. Then we know that this month, the a adults from last month will all have reproduced, so there will be a babies this month. How many adults will there be? Well the b babies from last month will all have grown up, and the a adults won’t have died because our rabbits live forever, so altogether there are now a+b adults. We have 2a+b rabbits in total. The number of adults, babies, and the total number of rabbits all follow the Fibonacci sequence, where each term is the sum of the previous two terms.
 But what have rabbits got to do with stacking cups?
But what have rabbits got to do with stacking cups?
Well let’s think about stacks in terms of right-way-up and upside-down cups. In the image, I have represented an upside-down cup in red, and a right-way-up cup in blue.
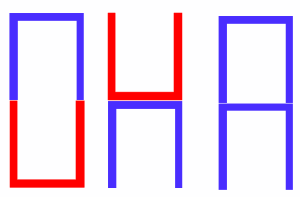
How many ways can we combine two
cups? There are three possibilities, shown in the image. I can have a blue cup on top of a red one, a red one on top of a blue one, or two blues on top of each other.
Now, I can use this to help me to work out the number of possibilities for three cups! I can imagine putting an extra cup on top of what I already have.
I can put a blue cup on top of any of my stacks, because I am always allowed to put a right-way-up cup on. So I get three stacks with blue on top. I am only allowed to put a red cup on top of a blue, because if I put red on red it nests inside instead of stacking, so I get two stacks with red on top.
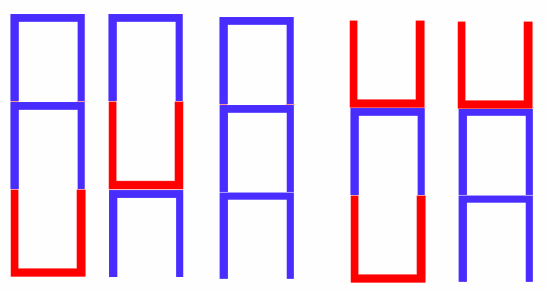
I want to make another table…
| Height of stack | Blue on top | Red on top | Total stacks |
| 1 | 1 | 1 | 2 |
| 2 | 2 | 1 | 3 |
| 3 | 3 | 2 | 5 |
| 4 | 5 | 3 | 8 |
| 5 | 8 | 5 | 13 |
| 6 | 13 | 8 | 21 |
| 7 | 21 | 13 | 34 |
| 8 | 34 | 21 | 55 |
In general, if I know there are a stacks of height n with blue on top, and b stacks of height n with red on top, then I can deduce that there are a+b stacks of height n+1 with blue on top (because I can put blue on top of anything), and there are a stacks of height n+1 with red on top (because I can only put red on top of blue), so there are 2a+b stacks of height n+1 altogether.
This is exactly the same logic as the rabbit problem, so structurally, they are the same! So the number of ways of stacking the cups gives the Fibonacci sequence! Neat, eh?

One Reply to “Stacking cups and bunny rabbits”
Comments are closed.